Stunning Tips About What Is The Current Division Rule In A Parallel Circuit

Understanding Current Division in Parallel Circuits
1. What is current division rule?
Ever wondered how electricity decides which path to take when it encounters a fork in the road, like a parallel circuit? Well, that's where the current division rule comes into play! It's a fundamental concept in electrical engineering that helps us understand how current splits itself among different branches in a parallel circuit. Think of it like this: imagine a river splitting into several smaller streams. The water (or in this case, the current) will naturally flow more strongly through the path of least resistance.
The current division rule is all about figuring out how much current flows through each of those streams. Specifically, it provides a formula to calculate the current through each branch of a parallel circuit based on the total current entering the junction and the resistance of each branch. Its a super handy tool for analyzing and designing electrical circuits — whether you're working on a complex project or just trying to understand how your home appliances work!
Without the current division rule, analyzing parallel circuits would be a complete headache. Imagine trying to guess how much current is flowing through each resistor in a complex network. It'd be like trying to predict the weather with just a gut feeling! This rule provides a precise and reliable method for calculating these currents, making circuit analysis much more manageable. It also helps in understanding how different components affect the overall circuit behavior, aiding in design and troubleshooting.
The core idea behind the current division rule is that current will always choose the path of least resistance. This is because electrons, being the lazy particles they are, prefer to flow where it's easiest. A lower resistance path means less opposition to the flow of electrons, so more current will flow through that branch. Conversely, a higher resistance path will see less current. It's like choosing between walking uphill and downhill — everyone prefers the downhill route!

The Formula
2. Current division formula explained with example
Alright, let's get down to the nitty-gritty (oops, almost slipped up there!). The current division rule has a specific formula that helps us calculate the current in each branch. The formula is: Ix = Itotal (Rtotal / Rx). Where: Ix is the current through the branch you're interested in (the one with resistance Rx). Itotal is the total current entering the parallel junction. Rx is the resistance of the specific branch you're analyzing. Rtotal is the equivalent resistance of the entire parallel circuit.
Calculating Rtotal is crucial. For a parallel circuit, the formula is: 1/Rtotal = 1/R1 + 1/R2 + 1/R3 + .... Once you calculate Rtotal, you can plug it into the first formula to find the current through any branch. Remember, the total resistance of a parallel circuit is always less than the smallest individual resistance. This makes sense, because adding parallel paths effectively increases the area available for current to flow.
Let's illustrate with an example. Imagine a parallel circuit with two resistors: R1 = 10 ohms and R2 = 20 ohms. The total current entering the junction is 3 amps. First, we need to find the equivalent resistance (Rtotal). 1/Rtotal = 1/10 + 1/20 = 3/20. Therefore, Rtotal = 20/3 = 6.67 ohms (approximately).
Now, let's find the current through R1 (I1). Using the formula: I1 = 3 amps (6.67 ohms / 10 ohms) = 2 amps (approximately). Similarly, for R2 (I2): I2 = 3 amps (6.67 ohms / 20 ohms) = 1 amp (approximately). Notice that more current flows through the 10-ohm resistor than the 20-ohm resistor, as expected! Also, I1 + I2 = 2 amps + 1 amp = 3 amps, which equals the total current entering the junction. This confirms our calculations!
Practical Applications: Where's This Useful?
3. Real-world uses of understanding current division
So, you might be thinking, "Okay, that's cool and all, but where am I actually going to use this in the real world?" Well, the current division rule isn't just some abstract concept confined to textbooks. It has numerous practical applications in electronics and electrical engineering. One common application is in the design of power distribution systems. Engineers use the current division rule to ensure that electrical power is distributed efficiently and safely to different parts of a building or a device.
Another important application is in designing circuits with specific current requirements. For example, imagine you need to power two LEDs, one requiring 20mA and the other requiring 30mA, from a single power supply. You can use the current division rule to design a parallel circuit with appropriate resistors to ensure that each LED receives the correct amount of current. Without this rule, you'd be guessing and potentially damaging the LEDs!
Current division principles also come into play in signal processing and telecommunications. When signals are split and routed through different paths, understanding how the current divides is essential for maintaining signal integrity and ensuring proper signal transmission. From audio amplifiers to radio receivers, the current division rule helps engineers design circuits that handle signals effectively and minimize losses.
Even in troubleshooting electrical problems, knowledge of current division can be invaluable. If a circuit isn't behaving as expected, understanding how the current should be distributed can help you identify faults and pinpoint the source of the problem. By measuring currents at different points in the circuit and comparing them to the calculated values, you can often diagnose issues like short circuits, open circuits, or component failures.
Current Division vs. Voltage Division: What's the Difference?
4. How current division is different from voltage division
It's easy to get current division and voltage division mixed up, especially since they both deal with how electrical quantities are distributed in a circuit. However, they apply to different circuit configurations and have different formulas. Current division, as we've discussed, applies to parallel circuits and determines how current splits among different branches. Voltage division, on the other hand, applies to series circuits and determines how voltage is distributed across different components.
In a series circuit, the total voltage is divided among the resistors based on their resistance values. The voltage division rule states that the voltage across a resistor is proportional to its resistance relative to the total resistance of the series circuit. The formula for voltage division is: Vx = Vtotal (Rx / Rtotal), where Vx is the voltage across resistor Rx, Vtotal is the total voltage, and Rtotal is the total resistance of the series circuit.
The key difference is that in a parallel circuit, the voltage is the same across all branches, while the current divides. In a series circuit, the current is the same through all components, while the voltage divides. Therefore, the current division rule is used for parallel circuits, and the voltage division rule is used for series circuits. Understanding this distinction is crucial for analyzing and designing different types of circuits.
Think of it like this: in a parallel circuit, you have multiple paths for the current to flow, so the current divides. In a series circuit, there's only one path for the current to flow, so the voltage divides. This simple analogy can help you remember which rule to apply in which situation. Also, remember that the total resistance calculation is different for series and parallel circuits, further emphasizing the distinction between the two scenarios.
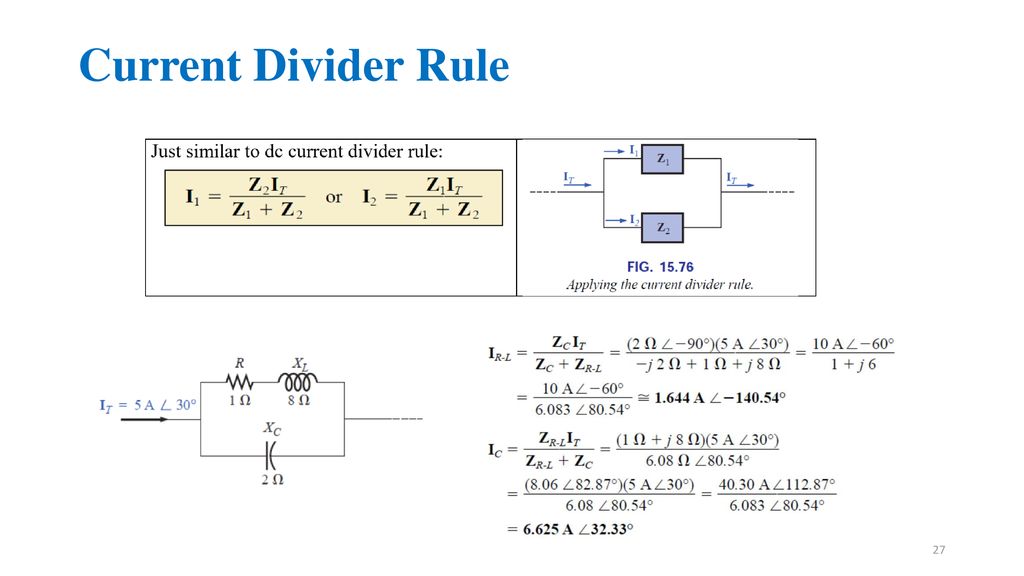
Chapter 15 Series And Parallel AC Circuits Ppt Download
Beyond the Basics
5. Factors that can affect current division rule
While the current division rule is a powerful tool, it's important to be aware of its limitations and the factors that can affect its accuracy. The rule assumes that the circuit consists of ideal resistors, meaning that their resistance values are constant and independent of factors like temperature or frequency. In reality, resistors can exhibit non-ideal behavior, especially at high frequencies or temperatures, which can affect the current distribution.
Another important consideration is the effect of internal resistance in voltage sources. The current division rule assumes that the voltage source is ideal, meaning that it has zero internal resistance. However, real-world voltage sources have some internal resistance, which can affect the total current and the current distribution in the parallel circuit. This effect is more pronounced when the internal resistance is a significant fraction of the total resistance in the circuit.
The presence of reactive components like capacitors and inductors can also complicate the analysis. The current division rule, as presented here, is valid only for DC circuits or AC circuits where the frequency is low enough that the reactive impedances of the capacitors and inductors are negligible. At higher frequencies, the reactive impedances become significant and must be taken into account when calculating the current distribution.
Finally, it's important to remember that the current division rule is based on Kirchhoff's Current Law (KCL), which states that the total current entering a junction must equal the total current leaving the junction. While KCL is a fundamental law of circuit theory, it relies on the assumption that there are no stray currents or leakage paths. In practice, there may be some small currents that are not accounted for in the analysis, which can introduce minor errors in the current distribution calculations.

Voltage And Current Division Circuits CircuitBread
FAQ
6. Frequently asked questions about current division
Q: Does the current division rule work for more than two parallel resistors?
A: Absolutely! The current division rule can be applied to any number of parallel resistors. You just need to make sure you correctly calculate the equivalent resistance of the entire parallel network before applying the formula. It's like dividing a pizza amongst multiple friends — the principle remains the same regardless of how many people are sharing!
Q: What happens if one of the resistors in a parallel circuit is zero ohms (a short circuit)?
A: If one of the resistors is a short circuit (zero ohms), all of the current will flow through that path. The other branches will effectively be bypassed, and no current will flow through them (assuming ideal components). It's like finding a super-fast shortcut — everyone will take it!
Q: Can I use the current division rule to find the voltage across a resistor in a parallel circuit?
A: While the current division rule directly gives you the current, you can easily find the voltage using Ohm's Law (V = IR). Since the voltage is the same across all branches in a parallel circuit, once you know the current through a resistor, you can calculate the voltage, which will be the same for all other resistors in the parallel network. It's like having a secret code to unlock all the circuit's secrets!

